
Security News
Research
Data Theft Repackaged: A Case Study in Malicious Wrapper Packages on npm
The Socket Research Team breaks down a malicious wrapper package that uses obfuscation to harvest credentials and exfiltrate sensitive data.
Implementation of special functions and distributions mathematical functions from the cephes library.
This is a WebAssembly packaging of the cephes library. The cephes library contains C implementations of most special functions, distributions, and other hard-to-implement mathematical functions.
Note that there are a few cephes functions that are not exposed here, as some of them are quite hard to make consumable in JavaScript using WebAssembly. Feel free to send a pull request if you need one of them.
npm install cephes
If you are looking on GitHub, you will notice some files are missing. These are statically built from the cephes library. See the CONTRIBUTING.md file, for how to build them.
Cephes is a WebAssembly module but is very small and fast to compile, as it doesn't depend on any runtime libraries. In Node.js it is therefore compiled synchronously and all you need to do is require the module.
const cephes = require('cephes'); // Node.js
In the browser, it is, for good practice, compiled asynchronously. You must
therefore wait for the .compiled promise to be resolved.
const cephes = require('cephes'); // Browser
await cephes.compiled;
Note that the .compiled promise is also available in Node.js, but it is
simply a dummy promise that resolves immediately.
There are three variations of functions to be aware of:
These don't require anything special.
const value = cephes.zeta(2, 1);
In C, these functions return a primary value and then return extra value using pointer arguments. In JavaScript this is implemented as a function that returns an array of length 2. The first element is the primary returned value, the second is an object of the extra returned values.
const [value, {ai, aip, bi, bip}] = cephes.airy(-1);
Some functions consumes an array of values, these must be TypedArrays of
the appropriate type. These functions will typically also require a variation
of .length value as a parameter, like you would do in C. Be aware, that in
some cases it may not be exactly the .length of the TypedArray, but may be
one less or one more. Check the specific function documentation to be sure.
const arrayInput = new Float64Array([2.2, 3.3, 4.4]);
const value = ephes.polevl(1.1, arrayInput, arrayInput.length - 1);
| Function | Description | Documentation |
|---|---|---|
| Arithmetic and Algebraic | ||
signbit(x) | Returns the sign bit | c-doc • js-doc |
isnan(x) | Check if Not-A-Number | c-doc • js-doc |
isfinite(x) | Check if finite | c-doc • js-doc |
cbrt(x) | Cube root | c-doc • js-doc |
polevl(x, coef, N) | Evaluate polynomial | c-doc • js-doc |
chbevl(x, array, n) | Evaluate Chebyshev series | c-doc • js-doc |
round(x) | Round to nearest integer value | c-doc • js-doc |
frexp(x) | Extract exponent | c-doc • js-doc |
ldexp(x, pw2) | Add integer to exponent | c-doc • js-doc |
| Exponential and Trigonometric | ||
expx2(x, sign) | Exponential of squared argument | c-doc • js-doc |
radian(d, m, s) | Degrees, minutes, seconds to radians | c-doc • js-doc |
sincos(x, flg) | Circular sine and cosine of argument in degrees | c-doc • js-doc |
cot(x) | Circular cotangent | c-doc • js-doc |
cotdg(x) | Circular cotangent of argument in degrees | c-doc • js-doc |
log1p(x) | Relative error approximations for log(1 + x) | c-doc • js-doc |
expm1(x) | Relative error approximations for exp(x) - 1 | c-doc • js-doc |
cosm1(x) | Relative error approximations for cos(x) - 1 | c-doc • js-doc |
acos(x) | Arc cosine | c-doc • js-doc |
acosh(x) | Arc hyperbolic cosine | c-doc • js-doc |
asinh(xx) | Arc hyperbolic sine | c-doc • js-doc |
atanh(x) | Arc hyperbolic tangent | c-doc • js-doc |
asin(x) | Arcsine | c-doc • js-doc |
atan(x) | Arctangent | c-doc • js-doc |
atan2(y, x) | Quadrant correct arctangent | c-doc • js-doc |
cos(x) | Cosine | c-doc • js-doc |
cosdg(x) | Cosine of arg in degrees | c-doc • js-doc |
exp(x) | Exponential, base e | c-doc • js-doc |
exp2(x) | Exponential, base 2 | c-doc • js-doc |
exp10(x) | Exponential, base 10 | c-doc • js-doc |
cosh(x) | Hyperbolic cosine | c-doc • js-doc |
sinh(x) | Hyperbolic sine | c-doc • js-doc |
tanh(x) | Hyperbolic tangent | c-doc • js-doc |
log(x) | Logarithm, base e | c-doc • js-doc |
log2(x) | Logarithm, base 2 | c-doc • js-doc |
log10(x) | Logarithm, base 10 | c-doc • js-doc |
pow(x, y) | Power | c-doc • js-doc |
powi(x, nn) | Integer Power | c-doc • js-doc |
sin(x) | Sine | c-doc • js-doc |
sindg(x) | Sine of arg in degrees | c-doc • js-doc |
tan(x) | Tangent | c-doc • js-doc |
tandg(x) | Tangent of arg in degrees | c-doc • js-doc |
| Exponential integral | ||
ei(x) | Exponential integral | c-doc • js-doc |
expn(n, x) | Exponential integral | c-doc • js-doc |
shichi(x) | Hyperbolic cosine integral | c-doc • js-doc |
sici(x) | Cosine integral | c-doc • js-doc |
| Gamma | ||
lbeta(a, b) | Natural log of |beta|. | c-doc • js-doc |
beta(a, b) | Beta | c-doc • js-doc |
fac(i) | Factorial | c-doc • js-doc |
gamma(x) | Gamma | c-doc • js-doc |
lgam(x) | Logarithm of gamma function | c-doc • js-doc |
incbet(aa, bb, xx) | Incomplete beta integral | c-doc • js-doc |
incbi(aa, bb, yy0) | Inverse beta integral | c-doc • js-doc |
igam(a, x) | Incomplete gamma integral | c-doc • js-doc |
igamc(a, x) | Complemented gamma integral | c-doc • js-doc |
igami(a, y0) | Inverse gamma integral | c-doc • js-doc |
psi(x) | Psi (digamma) function | c-doc • js-doc |
rgamma(x) | Reciprocal Gamma | c-doc • js-doc |
| Error function | ||
erf(x) | Error function | c-doc • js-doc |
erfc(a) | Complemented error function | c-doc • js-doc |
dawsn(xx) | Dawson's integral | c-doc • js-doc |
fresnl(xxa) | Fresnel integral | c-doc • js-doc |
| Bessel | ||
airy(x) | Airy | c-doc • js-doc |
j0(x) | Bessel, order 0 | c-doc • js-doc |
j1(x) | Bessel, order 1 | c-doc • js-doc |
jn(n, x) | Bessel, order n | c-doc • js-doc |
jv(n, x) | Bessel, noninteger order | c-doc • js-doc |
y0(x) | Bessel, second kind, order 0 | c-doc • js-doc |
y1(x) | Bessel, second kind, order 1 | c-doc • js-doc |
yn(n, x) | Bessel, second kind, order n | c-doc • js-doc |
yv(v, x) | Bessel, noninteger order | c-doc • js-doc |
i0(x) | Modified Bessel, order 0 | c-doc • js-doc |
i0e(x) | Exponentially scaled i0 | c-doc • js-doc |
i1(x) | Modified Bessel, order 1 | c-doc • js-doc |
i1e(x) | Exponentially scaled i1 | c-doc • js-doc |
iv(v, x) | Modified Bessel, nonint. order | c-doc • js-doc |
k0(x) | Mod. Bessel, 3rd kind, order 0 | c-doc • js-doc |
k0e(x) | Exponentially scaled k0 | c-doc • js-doc |
k1(x) | Mod. Bessel, 3rd kind, order 1 | c-doc • js-doc |
k1e(x) | Exponentially scaled k1 | c-doc • js-doc |
kn(nn, x) | Mod. Bessel, 3rd kind, order n | c-doc • js-doc |
| Hypergeometric | ||
hyperg(a, b, x) | Confluent hypergeometric | c-doc • js-doc |
hyp2f1(a, b, c, x) | Gauss hypergeometric function | c-doc • js-doc |
| Elliptic | ||
ellpe(x) | Complete elliptic integral | c-doc • js-doc |
ellie(phi, m) | Incomplete elliptic integral | c-doc • js-doc |
ellpk(x) | Complete elliptic integral | c-doc • js-doc |
ellik(phi, m) | Incomplete elliptic integral | c-doc • js-doc |
ellpj(u, m) | Jacobian elliptic function | c-doc • js-doc |
| Probability | ||
btdtr(a, b, x) | Beta distribution | c-doc • js-doc |
smirnov(n, e) | Exact Smirnov statistic, for one-sided test. | c-doc • js-doc |
kolmogorov(y) | Kolmogorov's limiting distribution of two-sided test. | c-doc • js-doc |
smirnovi(n, p) | Functional inverse of Smirnov distribution. | c-doc • js-doc |
kolmogi(p) | Functional inverse of Kolmogorov statistic for two-sided test. | c-doc • js-doc |
nbdtri(k, n, p) | Inverse Negative binomial distribution | c-doc • js-doc |
stdtri(k, p) | Functional inverse of Student's t distribution | c-doc • js-doc |
bdtr(k, n, p) | Binomial distribution | c-doc • js-doc |
bdtrc(k, n, p) | Complemented binomial | c-doc • js-doc |
bdtri(k, n, y) | Inverse binomial | c-doc • js-doc |
chdtr(df, x) | Chi square distribution | c-doc • js-doc |
chdtrc(df, x) | Complemented Chi square | c-doc • js-doc |
chdtri(df, y) | Inverse Chi square | c-doc • js-doc |
fdtr(ia, ib, x) | F distribution | c-doc • js-doc |
fdtrc(ia, ib, x) | Complemented F | c-doc • js-doc |
fdtri(ia, ib, y) | Inverse F distribution | c-doc • js-doc |
gdtr(a, b, x) | Gamma distribution | c-doc • js-doc |
gdtrc(a, b, x) | Complemented gamma | c-doc • js-doc |
nbdtr(k, n, p) | Negative binomial distribution | c-doc • js-doc |
nbdtrc(k, n, p) | Complemented negative binomial | c-doc • js-doc |
ndtr(a) | Normal distribution | c-doc • js-doc |
ndtri(y0) | Inverse normal distribution | c-doc • js-doc |
pdtr(k, m) | Poisson distribution | c-doc • js-doc |
pdtrc(k, m) | Complemented Poisson | c-doc • js-doc |
pdtri(k, y) | Inverse Poisson distribution | c-doc • js-doc |
stdtr(k, t) | Student's t distribution | c-doc • js-doc |
| Miscellaneous | ||
plancki(w, T) | Integral of Planck's black body radiation formula | c-doc • js-doc |
planckc(w, T) | Complemented Planck radiation integral | c-doc • js-doc |
planckd(w, T) | Planck's black body radiation formula | c-doc • js-doc |
planckw(T) | Wavelength, w, of maximum radiation at given temperature T. | c-doc • js-doc |
spence(x) | Dilogarithm | c-doc • js-doc |
zetac(x) | Riemann Zeta function | c-doc • js-doc |
zeta(x, q) | Two argument zeta function | c-doc • js-doc |
struve(v, x) | Struve function | c-doc • js-doc |
| Polynomials and Power Series | ||
p1evl(x, coef, N) | Evaluate polynomial when coefficient of x is 1.0. | c-doc • js-doc |
polylog(n, x) | The polylogarithm of order n | c-doc • js-doc |
signbit is the "Returns the sign bit". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#signbit.
const ret = cephes.signbit(x);
isnan is the "Check if Not-A-Number". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#isnan.
const ret = cephes.isnan(x);
isfinite is the "Check if finite". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#isfinite.
const ret = cephes.isfinite(x);
cbrt is the "Cube root". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#cbrt.
const ret = cephes.cbrt(x);
polevl is the "Evaluate polynomial". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#polevl.
const ret = cephes.polevl(x, new Float64Array(coef), N);
chbevl is the "Evaluate Chebyshev series". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#chbevl.
const ret = cephes.chbevl(x, new Float64Array(array), n);
round is the "Round to nearest integer value". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#round.
const ret = cephes.round(x);
frexp is the "Extract exponent". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#frexp.
const [ret, extra] = cephes.frexp(x);
The extra object contains the following values:
const {
pw2: int
} = extra;
ldexp is the "Add integer to exponent". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#ldexp.
const ret = cephes.ldexp(x, pw2);
expx2 is the "Exponential of squared argument". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#expx2.
const ret = cephes.expx2(x, sign);
radian is the "Degrees, minutes, seconds to radians". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#radian.
const ret = cephes.radian(d, m, s);
sincos is the "Circular sine and cosine of argument in degrees". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#sincos.
const [ret, extra] = cephes.sincos(x, flg);
The extra object contains the following values:
const {
s: double,
c: double
} = extra;
cot is the "Circular cotangent". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#cot.
const ret = cephes.cot(x);
cotdg is the "Circular cotangent of argument in degrees". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#cotdg.
const ret = cephes.cotdg(x);
log1p is the "Relative error approximations for log(1 + x)". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#log1p.
const ret = cephes.log1p(x);
expm1 is the "Relative error approximations for exp(x) - 1". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#expm1.
const ret = cephes.expm1(x);
cosm1 is the "Relative error approximations for cos(x) - 1". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#cosm1.
const ret = cephes.cosm1(x);
acos is the "Arc cosine". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#acos.
const ret = cephes.acos(x);
acosh is the "Arc hyperbolic cosine". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#acosh.
const ret = cephes.acosh(x);
asinh is the "Arc hyperbolic sine". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#asinh.
const ret = cephes.asinh(xx);
atanh is the "Arc hyperbolic tangent". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#atanh.
const ret = cephes.atanh(x);
asin is the "Arcsine". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#asin.
const ret = cephes.asin(x);
atan is the "Arctangent". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#atan.
const ret = cephes.atan(x);
atan2 is the "Quadrant correct arctangent". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#atan2.
const ret = cephes.atan2(y, x);
cos is the "Cosine". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#cos.
const ret = cephes.cos(x);
cosdg is the "Cosine of arg in degrees". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#cosdg.
const ret = cephes.cosdg(x);
exp is the "Exponential, base e". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#exp.
const ret = cephes.exp(x);
exp2 is the "Exponential, base 2". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#exp2.
const ret = cephes.exp2(x);
exp10 is the "Exponential, base 10". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#exp10.
const ret = cephes.exp10(x);
cosh is the "Hyperbolic cosine". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#cosh.
const ret = cephes.cosh(x);
sinh is the "Hyperbolic sine". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#sinh.
const ret = cephes.sinh(x);
tanh is the "Hyperbolic tangent". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#tanh.
const ret = cephes.tanh(x);
log is the "Logarithm, base e". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#log.
const ret = cephes.log(x);
log2 is the "Logarithm, base 2". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#log2.
const ret = cephes.log2(x);
log10 is the "Logarithm, base 10". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#log10.
const ret = cephes.log10(x);
pow is the "Power". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#pow.
const ret = cephes.pow(x, y);
powi is the "Integer Power". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#powi.
const ret = cephes.powi(x, nn);
sin is the "Sine". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#sin.
const ret = cephes.sin(x);
sindg is the "Sine of arg in degrees". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#sindg.
const ret = cephes.sindg(x);
tan is the "Tangent". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#tan.
const ret = cephes.tan(x);
tandg is the "Tangent of arg in degrees". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#tandg.
const ret = cephes.tandg(x);
ei is the "Exponential integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#ei.
const ret = cephes.ei(x);
expn is the "Exponential integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#expn.
const ret = cephes.expn(n, x);
shichi is the "Hyperbolic cosine integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#shichi.
const [ret, extra] = cephes.shichi(x);
The extra object contains the following values:
const {
si: double,
ci: double
} = extra;
sici is the "Cosine integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#sici.
const [ret, extra] = cephes.sici(x);
The extra object contains the following values:
const {
si: double,
ci: double
} = extra;
lbeta is the "Natural log of |beta|.". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#lbeta.
const ret = cephes.lbeta(a, b);
beta is the "Beta". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#beta.
const ret = cephes.beta(a, b);
fac is the "Factorial". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#fac.
const ret = cephes.fac(i);
gamma is the "Gamma". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#gamma.
const ret = cephes.gamma(x);
lgam is the "Logarithm of gamma function". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#lgam.
const ret = cephes.lgam(x);
incbet is the "Incomplete beta integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#incbet.
const ret = cephes.incbet(aa, bb, xx);
incbi is the "Inverse beta integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#incbi.
const ret = cephes.incbi(aa, bb, yy0);
igam is the "Incomplete gamma integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#igam.
const ret = cephes.igam(a, x);
igamc is the "Complemented gamma integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#igamc.
const ret = cephes.igamc(a, x);
igami is the "Inverse gamma integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#igami.
const ret = cephes.igami(a, y0);
psi is the "Psi (digamma) function". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#psi.
const ret = cephes.psi(x);
rgamma is the "Reciprocal Gamma". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#rgamma.
const ret = cephes.rgamma(x);
erf is the "Error function". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#erf.
const ret = cephes.erf(x);
erfc is the "Complemented error function". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#erfc.
const ret = cephes.erfc(a);
dawsn is the "Dawson's integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#dawsn.
const ret = cephes.dawsn(xx);
fresnl is the "Fresnel integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#fresnl.
const [ret, extra] = cephes.fresnl(xxa);
The extra object contains the following values:
const {
ssa: double,
cca: double
} = extra;
airy is the "Airy". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#airy.
const [ret, extra] = cephes.airy(x);
The extra object contains the following values:
const {
ai: double,
aip: double,
bi: double,
bip: double
} = extra;
j0 is the "Bessel, order 0". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#j0.
const ret = cephes.j0(x);
j1 is the "Bessel, order 1". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#j1.
const ret = cephes.j1(x);
jn is the "Bessel, order n". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#jn.
const ret = cephes.jn(n, x);
jv is the "Bessel, noninteger order". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#jv.
const ret = cephes.jv(n, x);
y0 is the "Bessel, second kind, order 0". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#y0.
const ret = cephes.y0(x);
y1 is the "Bessel, second kind, order 1". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#y1.
const ret = cephes.y1(x);
yn is the "Bessel, second kind, order n". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#yn.
const ret = cephes.yn(n, x);
yv is the "Bessel, noninteger order". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#yv.
const ret = cephes.yv(v, x);
i0 is the "Modified Bessel, order 0". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#i0.
const ret = cephes.i0(x);
i0e is the "Exponentially scaled i0". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#i0e.
const ret = cephes.i0e(x);
i1 is the "Modified Bessel, order 1". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#i1.
const ret = cephes.i1(x);
i1e is the "Exponentially scaled i1". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#i1e.
const ret = cephes.i1e(x);
iv is the "Modified Bessel, nonint. order". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#iv.
const ret = cephes.iv(v, x);
k0 is the "Mod. Bessel, 3rd kind, order 0". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#k0.
const ret = cephes.k0(x);
k0e is the "Exponentially scaled k0". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#k0e.
const ret = cephes.k0e(x);
k1 is the "Mod. Bessel, 3rd kind, order 1". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#k1.
const ret = cephes.k1(x);
k1e is the "Exponentially scaled k1". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#k1e.
const ret = cephes.k1e(x);
kn is the "Mod. Bessel, 3rd kind, order n". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#kn.
const ret = cephes.kn(nn, x);
hyperg is the "Confluent hypergeometric". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#hyperg.
const ret = cephes.hyperg(a, b, x);
hyp2f1 is the "Gauss hypergeometric function". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#hyp2f1.
const ret = cephes.hyp2f1(a, b, c, x);
ellpe is the "Complete elliptic integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#ellpe.
const ret = cephes.ellpe(x);
ellie is the "Incomplete elliptic integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#ellie.
const ret = cephes.ellie(phi, m);
ellpk is the "Complete elliptic integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#ellpk.
const ret = cephes.ellpk(x);
ellik is the "Incomplete elliptic integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#ellik.
const ret = cephes.ellik(phi, m);
ellpj is the "Jacobian elliptic function". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#ellpj.
const [ret, extra] = cephes.ellpj(u, m);
The extra object contains the following values:
const {
sn: double,
cn: double,
dn: double,
ph: double
} = extra;
btdtr is the "Beta distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#btdtr.
const ret = cephes.btdtr(a, b, x);
smirnov is the "Exact Smirnov statistic, for one-sided test.". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#smirnov.
const ret = cephes.smirnov(n, e);
kolmogorov is the "Kolmogorov's limiting distribution of two-sided test.". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#kolmogorov.
const ret = cephes.kolmogorov(y);
smirnovi is the "Functional inverse of Smirnov distribution.". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#smirnovi.
const ret = cephes.smirnovi(n, p);
kolmogi is the "Functional inverse of Kolmogorov statistic for two-sided test.". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#kolmogi.
const ret = cephes.kolmogi(p);
nbdtri is the "Inverse Negative binomial distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#nbdtri.
const ret = cephes.nbdtri(k, n, p);
stdtri is the "Functional inverse of Student's t distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#stdtri.
const ret = cephes.stdtri(k, p);
bdtr is the "Binomial distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#bdtr.
const ret = cephes.bdtr(k, n, p);
bdtrc is the "Complemented binomial". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#bdtrc.
const ret = cephes.bdtrc(k, n, p);
bdtri is the "Inverse binomial". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#bdtri.
const ret = cephes.bdtri(k, n, y);
chdtr is the "Chi square distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#chdtr.
const ret = cephes.chdtr(df, x);
chdtrc is the "Complemented Chi square". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#chdtrc.
const ret = cephes.chdtrc(df, x);
chdtri is the "Inverse Chi square". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#chdtri.
const ret = cephes.chdtri(df, y);
fdtr is the "F distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#fdtr.
const ret = cephes.fdtr(ia, ib, x);
fdtrc is the "Complemented F". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#fdtrc.
const ret = cephes.fdtrc(ia, ib, x);
fdtri is the "Inverse F distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#fdtri.
const ret = cephes.fdtri(ia, ib, y);
gdtr is the "Gamma distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#gdtr.
const ret = cephes.gdtr(a, b, x);
gdtrc is the "Complemented gamma". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#gdtrc.
const ret = cephes.gdtrc(a, b, x);
nbdtr is the "Negative binomial distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#nbdtr.
const ret = cephes.nbdtr(k, n, p);
nbdtrc is the "Complemented negative binomial". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#nbdtrc.
const ret = cephes.nbdtrc(k, n, p);
ndtr is the "Normal distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#ndtr.
const ret = cephes.ndtr(a);
ndtri is the "Inverse normal distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#ndtri.
const ret = cephes.ndtri(y0);
pdtr is the "Poisson distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#pdtr.
const ret = cephes.pdtr(k, m);
pdtrc is the "Complemented Poisson". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#pdtrc.
const ret = cephes.pdtrc(k, m);
pdtri is the "Inverse Poisson distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#pdtri.
const ret = cephes.pdtri(k, y);
stdtr is the "Student's t distribution". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#stdtr.
const ret = cephes.stdtr(k, t);
plancki is the "Integral of Planck's black body radiation formula". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#plancki.
const ret = cephes.plancki(w, T);
planckc is the "Complemented Planck radiation integral". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#planckc.
const ret = cephes.planckc(w, T);
planckd is the "Planck's black body radiation formula". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#planckd.
const ret = cephes.planckd(w, T);
planckw is the "Wavelength, w, of maximum radiation at given temperature T.". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#planckw.
const ret = cephes.planckw(T);
spence is the "Dilogarithm". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#spence.
const ret = cephes.spence(x);
zetac is the "Riemann Zeta function". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#zetac.
const ret = cephes.zetac(x);
zeta is the "Two argument zeta function". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#zeta.
const ret = cephes.zeta(x, q);
struve is the "Struve function". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#struve.
const ret = cephes.struve(v, x);
p1evl is the "Evaluate polynomial when coefficient of x is 1.0.". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#p1evl.
const ret = cephes.p1evl(x, new Float64Array(coef), N);
polylog is the "The polylogarithm of order n". You can read the full documentation at http://www.netlib.org/cephes/doubldoc.html#polylog.
const ret = cephes.polylog(n, x);
The cephes library, that this module wraps, can be found at http://www.netlib.org/cephes/. The cephes library from the NetLib website, doesn't have any license. However, the author Stephen Moshier, has kindly given permission for it to be included in a BSD-licensed package.
Please see the LICENSE file, for all the details.
FAQs
Implementation of special functions and distributions mathematical functions from the cephes library.
The npm package cephes receives a total of 30,100 weekly downloads. As such, cephes popularity was classified as popular.
We found that cephes demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 5 open source maintainers collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
Research
The Socket Research Team breaks down a malicious wrapper package that uses obfuscation to harvest credentials and exfiltrate sensitive data.
Research
Security News
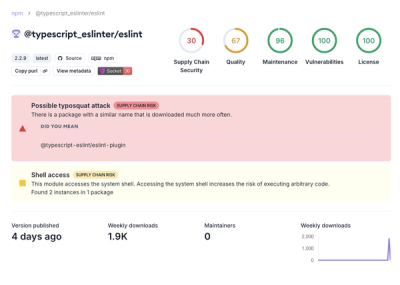
Attackers used a malicious npm package typosquatting a popular ESLint plugin to steal sensitive data, execute commands, and exploit developer systems.

Security News
The Ultralytics' PyPI Package was compromised four times in one weekend through GitHub Actions cache poisoning and failure to rotate previously compromised API tokens.